每日一题

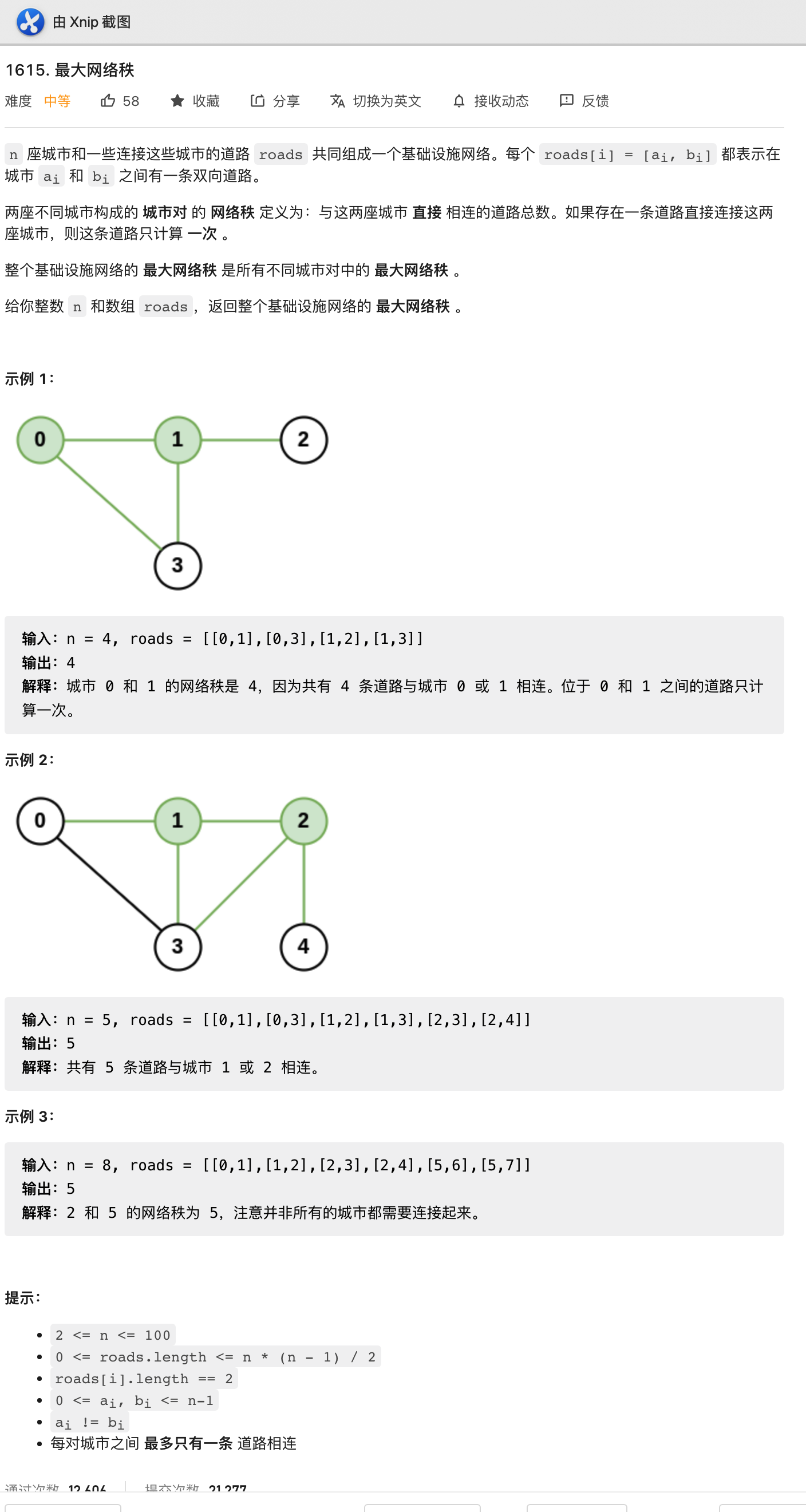
最大网络秩

/**
 * @param {number} n
 * @param {number[][]} roads
 * @return {number}
 */
var maximalNetworkRank = function(n, roads) {
    let arr = new Array(n).fill(0).map(() => new Array(n).fill(0))
    let degree = new Array(n).fill(0)
    let max = 0

    for(let item of roads){
        arr[item[0]][item[1]] = true
        arr[item[1]][item[0]] = true

        degree[item[0]]++
        degree[item[1]]++
    }


    for(let i=0;i<n;i++){
        for(let j=i+1;j<n;j++){
            let count = degree[i] + degree[j] - (arr[i][j] ? 1 : 0)
            max = Math.max(max, count)
        }
    }

    return max
};

礼物的最大价值（动态规划）

👉 本题 Leetcode 链接-47在新窗口打开

在一个 m*n 的棋盘的每一格都放有一个礼物，每个礼物都有一定的价值（价值大于 0）。你可以从棋盘的左上角开始拿格子里的礼物，并每次向右或者向下移动一格、直到到达棋盘的右下角。给定一个棋盘及其上面的礼物的价值，请计算你最多能拿到多少价值的礼物？

示例 1:
- 输入: [ [1,3,1], [1,5,1], [4,2,1] ]
- 输出: 12
- 解释: 路径 1→3→5→2→1 可以拿到最多价值的礼物

function maxValue(grid: number[][]): number {
    let row = grid.length, column = grid[0].length, arr = new Array(row).fill(0).map(() => (new Array(column).fill(0)))

    for(let i=0;i<row;i++){
        for(let j=0;j<column;j++){
            if(i>0){
                arr[i][j]= Math.max(arr[i][j], arr[i-1][j])
            }
            if(j>0){
                arr[i][j]= Math.max(arr[i][j], arr[i][j-1])
            }

            arr[i][j] += grid[i][j]
        }
    }

    return arr[row-1][column-1]
};

得到 K 个黑块的最少涂色次数(滑动窗口)

👉 本题 Leetcode 链接-2379在新窗口打开

给你一个长度为 n 下标从 0 开始的字符串 blocks ，blocks[i] 要么是 'W' 要么是 'B' ，表示第 i 块的颜色。字符 'W' 和 'B' 分别表示白色和黑色。

给你一个整数 k ，表示想要连续黑色块的数目。

每一次操作中，你可以选择一个白色块将它涂成黑色块。

请你返回至少出现一次连续 k 个黑色块的最少操作次数。

示例 1：
- 输入：blocks = "WBBWWBBWBW", k = 7
- 输出：3
- 解释：一种得到 7 个连续黑色块的方法是把第 0 ，3 和 4 个块涂成黑色。得到 blocks = "BBBBBBBWBW" 。可以证明无法用少于 3 次操作得到 7 个连续的黑块。所以我们返回 3 。
示例 2：
- 输入：blocks = "WBWBBBW", k = 2
- 输出：0
- 解释：不需要任何操作，因为已经有 2 个连续的黑块。所以我们返回 0 。

维护一个长度为 k 的滑动窗口，记录需要涂成黑色块的白色块的最少个数

function minimumRecolors(blocks: string, k: number): number {
    let count = 0
    for(let i=0;i<k;i++){
        count += blocks[i] === 'W' ? 1 : 0
    }

    let res = count

    for(let i=k;i<blocks.length;i++){
        count += blocks[i] === 'W' ? 1: 0
        count -= blocks[i-k] === 'W' ? 1 : 0
        res = Math.min(res, count)
    }

    return res
};

保证文件名唯一

👉 本题 Leetcode 链接-0502在新窗口打开

给你一个长度为 n 的字符串数组 names 。你将会在文件系统中创建 n 个文件夹：在第 i 分钟，新建名为 names[i] 的文件夹。

由于两个文件不能共享相同的文件名，因此如果新建文件夹使用的文件名已经被占用，系统会以 (k) 的形式为新文件夹的文件名添加后缀，其中 k 是能保证文件名唯一的最小正整数。

返回长度为 n 的字符串数组，其中 ans[i] 是创建第 i 个文件夹时系统分配给该文件夹的实际名称。

示例1
- 输入：names = ["gta","gta(1)","gta","avalon"]
- 输出：["gta","gta(1)","gta(2)","avalon"]
- 解释：文件系统将会这样创建文件名： "gta" --> 之前未分配，仍为 "gta" "gta(1)" --> 之前未分配，仍为 "gta(1)" "gta" --> 文件名被占用，系统为该名称添加后缀 (k)，由于 "gta(1)" 也被占用，所以 k = 2 。实际创建的文件名为 "gta(2)" 。 "avalon" --> 之前未分配，仍为 "avalon"
示例2
- 输入：names = ["kaido","kaido(1)","kaido","kaido(1)"]
- 输出：["kaido","kaido(1)","kaido(2)","kaido(1)(1)"]
- 解释：注意，如果含后缀文件名被占用，那么系统也会按规则在名称后添加新的后缀 (k) 。

function getFolderNames(names: string[]): string[] {
    let map = new Map(), res = []

    for(let name of names){
        if(!map.has(name)){
            map.set(name, 1)
        } else {
            let val = map.get(name)
            while(map.has(getName(name,val))) {val++}

            map.set(getName(name,val), 1 )
            map.set(name, val+1)
        }
    }

    for(let [key, value] of map.entries()){
        res.push(key)
    }

    return res
};

function getName(name: string,val: number): string{
    return name + '('+ val +')'
}

二进制数

👉 本题 Leetcode 链接-0502在新窗口打开

二进制数转字符串。给定一个介于0和1之间的实数（如0.72），类型为double，打印它的二进制表达式。如果该数字无法精确地用32位以内的二进制表示，则打印“ERROR”。

示例1:
- 输入：0.625
- 输出："0.101"
示例2:
- 输入：0.1
- 输出："ERROR"
- 提示：0.1无法被二进制准确表示

任何进制表示的小数，乘上进制等价于小数点往右移一位

function printBin(num: number): string {
    let sb = '0.';
    
    while (sb.length <= 32 && num !== 0) {
        num *= 2;
        const digit = Math.floor(num);
        sb += digit;
        num -= digit;
    }

    return sb.length <= 32 ? sb : "ERROR";
};

堆叠长方体的最大高度

👉 本题 Leetcode 链接-1691在新窗口打开

给你 n 个长方体 cuboids ，其中第 i 个长方体的长宽高表示为 cuboids[i] = [widthi, lengthi, heighti]（下标从 0 开始）。请你从 cuboids 选出一个子集，并将它们堆叠起来。

如果 widthi <= widthj 且 lengthi <= lengthj 且 heighti <= heightj ，你就可以将长方体 i 堆叠在长方体 j 上。你可以通过旋转把长方体的长宽高重新排列，以将它放在另一个长方体上。

返回堆叠长方体 cuboids 可以得到的最大高度。

示例

示例 1：
- 输入：cuboids = [[50,45,20],[95,37,53],[45,23,12]]
- 输出：190
- 解释：
  - 第 1 个长方体放在底部，53x37 的一面朝下，高度为 95 。
  - 第 0 个长方体放在中间，45x20 的一面朝下，高度为 50 。
  - 第 2 个长方体放在上面，23x12 的一面朝下，高度为 45 。
  - 总高度是 95 + 50 + 45 = 190 。
示例 2：
- 输入：cuboids = [[38,25,45],[76,35,3]]
- 输出：76
- 解释：无法将任何长方体放在另一个上面。选择第 1 个长方体然后旋转它，使 35x3 的一面朝下，其高度为 76 。

思路

动态规划&排序

先将长方体数组 cuboids 内的每个长方体长宽高按照长度大小进行排序
再将长方体数组 cuboids 整体按照和大小排序
根据题意，我们需要返回堆叠长方体 cuboids 的最大高度，我们可以知道，对于求子集问题，我们可以采用动态规划进行求解，转移方程如下

$$f(x) = Math.max(f(x), f(y) + height)$$

其中，f(y)为满足条件的堆叠长方体和height之和。

最后返回 $f(x)$最大值

function maxHeight(cuboids: number[][]): number {
    let len = cuboids.length,
        dp = new Array(len).fill(-1);

    for (let cuboid of cuboids) {
        cuboid.sort((a, b) => a - b);
    }

    cuboids.sort((a, b) => a[0] + a[1] + a[2] - (b[0] + b[1] + b[2]));

    for (let i = 0; i < len; i++) {
        dp[i] = cuboids[i][2];
        for (let j = 0; j < i; j++) {
            if (
                cuboids[i][0] >= cuboids[j][0] &&
                cuboids[i][1] >= cuboids[j][1] &&
                cuboids[i][2] >= cuboids[j][2]
            ) {
                dp[i] = Math.max(dp[i], dp[j] + cuboids[i][2]);
            }
        }
    }

    return Math.max(...dp);
}

一个数字是否可以表示成三的幂的和

给你一个整数 n ，如果你可以将 n 表示成若干个不同的三的幂之和，请你返回 true ，否则请返回 false 。

对于一个整数 y ，如果存在整数 x 满足 y == 3x ，我们称这个整数 y 是三的幂。

示例

示例 1：
- 输入：n = 12
- 输出：true
- 解释：12 = 31 + 32
示例 2：
- 输入：n = 91
- 输出：true
- 解释：91 = 30 + 32 + 34
示例 3：
- 输入：n = 21
- 输出：false

思路

将 n 转换成 3 进制，对应的数字应该只有 0 和 1。

代码

function checkPowersOfThree(n: number): boolean {
    while (n) {
        if (n % 3 === 2) return false;

        n = Math.floor(n / 3);
    }
    return true;
}

最大频率栈

👉 本题 Leetcode 链接-895在新窗口打开

题目说明

设计一个类似堆栈的数据结构，将元素推入堆栈，并从堆栈中弹出出现频率最高的元素。

实现 FreqStack 类:

FreqStack() 构造一个空的堆栈。
void push(int val) 将一个整数 val 压入栈顶。
int pop() 删除并返回堆栈中出现频率最高的元素。如果出现频率最高的元素不只一个，则移除并返回最接近栈顶的元素。

输入输出

示例 1：
- 输入：["FreqStack","push","push","push","push","push","push","pop","pop","pop","pop"], [[],[5],[7],[5],[7],[4],[5],[],[],[],[]]
- 输出：[null,null,null,null,null,null,null,5,7,5,4]
- 解释：
  - FreqStack = new FreqStack();
  - freqStack.push (5);//堆栈为 [5]
  - freqStack.push (7);//堆栈是 [5,7]
  - freqStack.push (5);//堆栈是 [5,7,5]
  - freqStack.push (7);//堆栈是 [5,7,5,7]
  - freqStack.push (4);//堆栈是 [5,7,5,7,4]
  - freqStack.push (5);//堆栈是 [5,7,5,7,4,5]
  - freqStack.pop ();//返回 5 ，因为 5 出现频率最高。堆栈变成 [5,7,5,7,4]。
  - freqStack.pop ();//返回 7 ，因为 5 和 7 出现频率最高，但 7 最接近顶部。堆栈变成 [5,7,5,4]。
  - freqStack.pop ();//返回 5 ，因为 5 出现频率最高。堆栈变成 [5,7,4]。
  - freqStack.pop ();//返回 4 ，因为 4, 5 和 7 出现频率最高，但 4 是最接近顶部的。堆栈变成 [5,7]。

解题思路

通用哈希解法

使用 map 保存所有数字及其对应的出现次数（频率）
使用 group 保存所有出现次数（频率）及其对应数字，主要用于 pop 时弹出栈顶元素
使用 max 记录最大出现次数，pop 时判断其 group 是否为空，为空时 max 需要减 1。

代码实现

class FreqStack {
    private map: Map<number, number>;
    private group: Map<number, Array<number>>;
    private max: number;

    constructor() {
        this.map = new Map();
        this.group = new Map();
        this.max = 0;
    }

    push(val: number): void {
        this.map.set(val, (this.map.get(val) ?? 0) + 1);
        if (!this.group.has(this.map.get(val))) {
            this.group.set(this.map.get(val), []);
        }

        this.group.get(this.map.get(val)).push(val);
        this.max = Math.max(this.max, this.map.get(val));
    }

    pop(): number {
        let ans = this.group.get(this.max)[this.group.get(this.max).length - 1];
        this.map.set(ans, this.map.get(ans) - 1);
        this.group.get(this.max).pop();

        if (this.group.get(this.max).length === 0) {
            this.max--;
        }

        return ans;
    }
}

第 N 个神奇数字

👉 本题 Leetcode 链接-878在新窗口打开

题目说明

一个正整数如果能被 a 或 b 整除，那么它是神奇的。

给定三个整数 n , a , b ，返回第 n 个神奇的数字。因为答案可能很大，所以返回答案对 109 + 7 取模后的值。

输入输出

示例 1：
- 输入：n = 1, a = 2, b = 3
- 输出：2
示例 2：
- 输入：n = 4, a = 2, b = 3
- 输出：6

$1 <= n <= 109; 2 <= a, b <= 4 * 104$

解题思路

核心思路是二分法+容斥原理

我们假设$f(x)$表示为小于等于 x 的「神奇数字」个数，因为小于等于 x 中能被 a 整除的数的个数为 $x/a$，小于等于 x 中能被 b 整除的数的个数为 $x/b$，小于等于 x 中同时能被 a 和 b 整除的数的个数为 $x/c$，其中 c 为 a 和 b 的最小公倍数 $$f(x)=x/a + x/b - x/c$$

$f(x)$是一个单调递增函数

计算最小公倍数

// 最大公约数
function gcd(a: number, b: number): number {
    return b == 0 ? a : gcd(b, a % b);
}

// 最小公倍数
function lcm(a: number, b: number): number {
    return Math.floor((a * b) / gcd(a, b));
}

代码实现

function nthMagicalNumber(n: number, a: number, b: number): number {
    let mod = 10 ** 9 + 7,
        left = Math.min(a, b),
        right = n * Math.min(a, b),
        lcmNum = lcm(a, b);

    while (left < right) {
        const mid = Math.floor((right + left) / 2);

        if (getCount(mid, a, b, lcmNum) >= n) right = mid;
        else left = mid + 1;
    }
    return right % mod;
}

function gcd(a: number, b: number): number {
    return b == 0 ? a : gcd(b, a % b);
}

function lcm(a: number, b: number): number {
    return Math.floor((a * b) / gcd(a, b));
}

function getCount(x: number, a: number, b: number, c: number): number {
    return Math.floor(x / a) + Math.floor(x / b) - Math.floor(x / c);
}

分汤

👉 本题 Leetcode 链接-808在新窗口打开

题目说明

有 A 和 B 两种类型的汤。一开始每种类型的汤有 n 毫升。有四种分配操作：

提供 100ml 的汤 A 和 0ml 的汤 B。提供 75ml 的汤 A 和 25ml 的汤 B 。提供 50ml 的汤 A 和 50ml 的汤 B 。提供 25ml 的汤 A 和 75ml 的汤 B 。当我们把汤分配给某人之后，汤就没有了。每个回合，我们将从四种概率同为 0.25 的操作中进行分配选择。如果汤的剩余量不足以完成某次操作，我们将尽可能分配。当两种类型的汤都分配完时，停止操作。

注意不存在先分配 100 ml 汤 B 的操作。

需要返回的值：汤 A 先分配完的概率 + 汤 A 和汤 B 同时分配完的概率/2。返回值在正确答案 10^-5 的范围内将被认为是正确的。

输入输出

示例 1: - 输入: n = 50 - 输出: 0.62500 - 解释: 如果我们选择前两个操作，A 首先将变为空。对于第三个操作，A 和 B 会同时变为空。对于第四个操作，B 首先将变为空。所以 A 变为空的总概率加上 A 和 B 同时变为空的概率的一半是 0.25 *(1 + 1 + 0.5 + 0)= 0.625。
示例 2:
- 输入: n = 100
- 输出: 0.71875

解题思路

核心思路是动态规划+数学期望（对于较大值而言）

动态规划部分

先简化下本题目模型，将 n 除以 25，分配操作变为[4,0]、[3,1]、[2,2]、[1,2]四种组合且每种组合概率为 0.25。

根据题意需要返回的汤 A 先分配完的概率+汤A和汤 B 同时分配完的概率/2。可以计算其动态转移方程为

$$dp(i,j)$$ 表示汤 A 和汤 B 分别剩下 i 和 j 份时的概率值

$$dp(i,j)=0.25 * (dp(i−4,j)+dp(i−3,j−1)+dp(i−2,j−2)+dp(i−1,j−3))$$

当 i > 0 && j = 0 时, $dp(i,j)=0$
当 i = 0 && j = 0 时，$dp(i,j)=0.5$
当 i = 0 && j > 0 时，$dp(i,j)=1$

由于要分别讨论 i 和 j 的情况，因此时间复杂度是 $O(n^2)$。当 n 取值较大时，可能会超时。

期望部分

通过数学期望值我们可以计算，汤 A 平均会被分配的份数期望为 $E(A) = (4+3+2+1) * 0.25 = 2.5$，汤 B 平均会被分配的份数期望为 $E(B) = (0+1+2+3) * 0.25 = 1.5$，因此，当 n 值较大时，汤 A 被先取完的概率会更接近 1，通过计算我们可以取 179 作为分解值，即 n>179 时直接返回 1。计算过程

$soupServings(178*25) = 0.9999893866772255$
$soupServings(179*25) = 0.9999902113072541$

根据题意返回值在正确答案 $10^{-5}$ 的范围内将被认为是正确的，因此可以选择 179 作为临界值。

代码实现

function soupServings(n: number): number {
    n = Math.ceil(n / 25);

    if (n >= 200) {
        return 1.0;
    }

    let dp = new Array(n + 1).fill(0).map(() => new Array(n + 1).fill(0));

    return dfs(dp, n, n);
}

const dfs = (cache: Array<Array<number>>, a: number, b: number): number => {
    if (a <= 0 && b <= 0) {
        return 0.5;
    } else if (a <= 0) {
        return 1;
    } else if (b <= 0) {
        return 0;
    }

    if (cache[a][b] === 0) {
        cache[a][b] =
            0.25 *
            (dfs(cache, a - 4, b) +
                dfs(cache, a - 3, b - 1) +
                dfs(cache, a - 2, b - 2) +
                dfs(cache, a - 1, b - 3));
    }

    return cache[a][b];
};

香槟塔

👉 本题 Leetcode 链接-在新窗口打开

题目说明

我们把玻璃杯摆成金字塔的形状，其中第一层有 1 个玻璃杯，第二层有 2 个，依次类推到第 100 层，每个玻璃杯 (250ml) 将盛有香槟。

从顶层的第一个玻璃杯开始倾倒一些香槟，当顶层的杯子满了，任何溢出的香槟都会立刻等流量的流向左右两侧的玻璃杯。当左右两边的杯子也满了，就会等流量的流向它们左右两边的杯子，依次类推。（当最底层的玻璃杯满了，香槟会流到地板上）

例如，在倾倒一杯香槟后，最顶层的玻璃杯满了。倾倒了两杯香槟后，第二层的两个玻璃杯各自盛放一半的香槟。在倒三杯香槟后，第二层的香槟满了 - 此时总共有三个满的玻璃杯。在倒第四杯后，第三层中间的玻璃杯盛放了一半的香槟，他两边的玻璃杯各自盛放了四分之一的香槟，如下图所示。

现在当倾倒了非负整数杯香槟后，返回第 i 行 j 个玻璃杯所盛放的香槟占玻璃杯容积的比例（ i 和 j 都从 0 开始）。

输入输出

示例 1:
- 输入: poured(倾倒香槟总杯数) = 1, query_glass(杯子的位置数) = 1, query_row(行数) = 1
- 输出: 0.00000
- 解释: 我们在顶层（下标是（0，0））倒了一杯香槟后，没有溢出，因此所有在顶层以下的玻璃杯都是空的。
示例 2:
- 输入: poured(倾倒香槟总杯数) = 2, query_glass(杯子的位置数) = 1, query_row(行数) = 1
- 输出: 0.50000
- 解释: 我们在顶层（下标是（0，0）倒了两杯香槟后，有一杯量的香槟将从顶层溢出，位于（1，0）的玻璃杯和（1，1）的玻璃杯平分了这一杯香槟，所以每个玻璃杯有一半的香槟。
示例 3:
- 输入: poured = 100000009, query_row = 33, query_glass = 17
- 输出: 1.00000

解题思路

每层杯子的数量是query_row + 1，其对应的流量都是总流量减去上层所有流量后的平均值
可以先计算从第 i 行开始的溢出量 others
继续模拟将第 i+1 行的所有杯子装满所流经的流量
返回其比例大小 ratio，如果 ratio 大于 1，则返回 1，因为它最大容量为 1，多余的流量已流到下一层

代码实现

function champagneTower(
    poured: number,
    query_row: number,
    query_glass: number
): number {
    let arr = [poured],
        ratio = 0;

    for (let i = 1; i < query_row + 1; i++) {
        let others = Math.max(0, arr[0] - 1);
        arr[0] = 0;

        for (let j = 0; j < i; j++) {
            let half = others / 2;
            arr[j] += half;
            others = Math.max(0, arr[j + 1] - 1);
            arr[j + 1] = half;
        }
    }

    ratio = arr[query_glass];

    if (ratio > 1) return 1;

    return ratio;
}

自定义字符串排序

👉 本题 Leetcode 链接-在新窗口打开

题目说明

给定两个字符串 order 和 s。order 的所有字母都是唯一的，并且以前按照一些自定义的顺序排序。

对 s 的字符进行置换，使其与排序的 order 相匹配。更具体地说，如果在 order 中的字符 x 出现字符 y 之前，那么在排列后的字符串中， x 也应该出现在 y 之前。

返回满足这个性质的 s 的任意一种排列。

输入输出

示例 1: - 输入: order = "cba", s = "abcd" - 输出: "cbad" - 解释: “a”、“b”、“c”是按顺序出现的，所以“a”、“b”、“c”的顺序应该是“c”、“b”、“a”。因为“d”不是按顺序出现的，所以它可以在返回的字符串中的任何位置。“dcba”、“cdba”、“cbda”也是有效的输出。
示例 2:
- 输入: order = "cbafg", s = "abcd"
- 输出: "cbad"

解题思路

使用 map 统计 s 中字符出现的次数
按照 order 顺序遍历并返回所有符合要求的字符串，多个相同的字符串直接 repeat 其数量即可
继续遍历字符串 s,对于 order 中不存在的字符直接拼接在其后返回

代码实现

function customSortString(order: string, s: string): string {
    let res = "",
        map = new Map<string, number>();

    for (let char of s) {
        if (map.has(char)) {
            map.set(char, map.get(char)! + 1);
        } else {
            map.set(char, 1);
        }
    }

    for (let char of order) {
        if (map.has(char)) res += char.repeat(map.get(char)!);
    }

    for (let char of s) {
        if (order.indexOf(char) === -1) res += char;
    }

    return res;
}

解析布尔表达式

👉 Leetcode 链接-1106在新窗口打开

给你一个以字符串形式表述的布尔表达式（boolean） expression，返回该式的运算结果。

有效的表达式需遵循以下约定：

"t"，运算结果为 True
"f"，运算结果为 False
"!(expr)"，运算过程为对内部表达式 expr 进行逻辑非的运算（NOT）
"&(expr1,expr2,...)"，运算过程为对 2 个或以上内部表达式 expr1, expr2, ... 进行逻辑与的运算（AND）
"|(expr1,expr2,...)"，运算过程为对 2 个或以上内部表达式 expr1, expr2, ... 进行逻辑或的运算（OR）

function parseBoolExpr(expression: string): boolean {
    let stack = [],
        len = expression.length;

    for (let i = 0; i < len; i++) {
        const char = expression[i];
        if (char === ",") {
            continue;
        } else if (char !== ")") {
            stack.push(char);
        } else {
            let t = 0,
                f = 0;

            while (stack[stack.length - 1] !== "(") {
                const val = stack.pop();
                if (val === "t") {
                    t++;
                } else {
                    f++;
                }
            }

            stack.pop();
            const peek = stack.pop();
            switch (peek) {
                case "!":
                    stack.push(f === 1 ? "t" : "f");
                    break;
                case "&":
                    stack.push(f === 0 ? "t" : "f");
                    break;
                case "|":
                    stack.push(t > 0 ? "t" : "f");
                    break;
                default:
            }
        }
    }

    return stack.pop() === "t";
}

链表组件

👉 Leetcode 链接-817在新窗口打开给定链表头结点 head，该链表上的每个结点都有一个唯一的整型值。同时给定列表 nums，该列表是上述链表中整型值的一个子集。

返回列表 nums 中组件的个数，这里对组件的定义为：链表中一段最长连续结点的值（该值必须在列表 nums 中）构成的集合。

/**
 * Definition for singly-linked list.
 * class ListNode {
 *     val: number
 *     next: ListNode | null
 *     constructor(val?: number, next?: ListNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.next = (next===undefined ? null : next)
 *     }
 * }
 */

function numComponents(head: ListNode | null, nums: number[]): number {
    let ans = 0;
    const set = new Set();

    for (const x of nums) set.add(x);

    while (head !== null) {
        if (set.has(head.val)) {
            while (head !== null && set.has(head.val)) {
                head = head.next;
            }
            ans++;
        } else {
            head = head.next;
        }
    }

    return ans;
}

按照频率将数组升序排序

👉 Leetcode 链接-1636在新窗口打开

给你一个整数数组 nums ，请你将数组按照每个值的频率升序排序。如果有多个值的频率相同，请你按照数值本身将它们降序排序。

请你返回排序后的数组。

示例 1：
- 输入：nums = [1,1,2,2,2,3]
- 输出：[3,1,1,2,2,2]
- 解释：'3' 频率为 1，'1' 频率为 2，'2' 频率为 3 。
示例 2：
- 输入：nums = [2,3,1,3,2]
- 输出：[1,3,3,2,2]
- 解释：'2' 和 '3' 频率都为 2 ，所以它们之间按照数值本身降序排序。

function frequencySort(nums: number[]): number[] {
    let map = new Map<number, number>();

    for (let num of nums) {
        if (map.has(num)) {
            let count = map.get(num) + 1;
            map.set(num, count);
        } else {
            map.set(num, 0);
        }
    }

    nums.sort((a, b) => {
        return map.get(a) != map.get(b) ? map.get(a) - map.get(b) : b - a;
    });

    return nums;
}

两个相同字符之间的最长子字符串

👉 Leetcode 链接-1624在新窗口打开

给你一个字符串 s，请你返回两个相同字符之间的最长子字符串的长度，计算长度时不含这两个字符。如果不存在这样的子字符串，返回 -1 。

子字符串是字符串中的一个连续字符序列。

考点

哈希表

function maxLengthBetweenEqualCharacters(s: string): number {
    let count = -1,
        len = s.length,
        map = new Map();

    for (let i = 0; i < len; i++) {
        let char = s[i];

        if (map[char] !== undefined) {
            count = Math.max(count, i - map[char] - 1);
        } else {
            map[char] = i;
        }
    }

    return count;
}

最大交换

👉 Leetcode 链接-670在新窗口打开

给定一个非负整数，你至多可以交换一次数字中的任意两位。返回你能得到的最大值。

给定数字的范围是 [0, 108]

示例 1 :
- 输入: 2736
- 输出: 7236
- 解释: 交换数字 2 和数字 7。
示例 2 :
- 输入: 9973
- 输出: 9973
- 解释: 不需要交换

考点

贪心算法

暴力解法

var maximumSwap = function (num) {
    let numStr = String(num),
        arr = [...numStr],
        len = numStr.length,
        max = num;

    for (let i = 0; i < len; i++) {
        for (let j = i + 1; j < len; j++) {
            swap(arr, i, j);
            max = Math.max(max, parseInt(arr.join("")));
            swap(arr, i, j);
        }
    }

    return max;
};

function swap(arr, i, j) {
    let temp = arr[i];
    arr[i] = arr[j];
    arr[j] = temp;
}

贪心解法 ⭐⭐

/**
 * @param {number} num
 * @return {number}
 */
var maximumSwap = function (num) {
    let numStr = String(num),
        arr = [...numStr],
        len = arr.length;
    let maxIndex = len - 1,
        sid1 = -1,
        sid2 = -1;

    // 从右向左遍历找最大的数字，记录索引，同时如果左边的数字比右边的小，也记录其索引
    for (let i = len - 1; i >= 0; i--) {
        if (arr[i] > arr[maxIndex]) {
            maxIndex = i;
        } else if (arr[i] < arr[maxIndex]) {
            sid1 = i;
            sid2 = maxIndex;
        }
    }

    // 存在左边的数字比右边的小，交换右边最大的数字位置到左边
    if (sid1 > -1) {
        [arr[sid1], arr[sid2]] = [arr[sid2], arr[sid1]];
        return parseInt(arr.join(""));
    }

    return num;
};

雇佣 K 名工人的最低成本 ⭐⭐⭐

👉 Leetcode 链接-857在新窗口打开

有 n 名工人。给定两个数组 quality 和 wage ，其中，quality[i] 表示第 i 名工人的工作质量，其最低期望工资为 wage[i] 。

现在我们想雇佣 k 名工人组成一个工资组。在雇佣一组 k 名工人时，我们必须按照下述规则向他们支付工资：

对工资组中的每名工人，应当按其工作质量与同组其他工人的工作质量的比例来支付工资。工资组中的每名工人至少应当得到他们的最低期望工资。给定整数 k ，返回组成满足上述条件的付费群体所需的最小金额。在实际答案的 10-5 以内的答案将被接受。。

考点

最大队列在新窗口打开

/**
 * @param {number[]} quality
 * @param {number[]} wage
 * @param {number} k
 * @return {number}
 */
var mincostToHireWorkers = function (quality, wage, k) {
    const len = quality.length,
        arr = new Array(len).fill(0).map((_, i) => i);
    arr.sort((a, b) => {
        return quality[b] * wage[a] - quality[a] * wage[b];
    });

    let ans = Infinity,
        total = 0,
        pq = new MaxPriorityQueue();

    for (let i = 0; i < k - 1; i++) {
        total += quality[arr[i]];
        pq.enqueue(quality[arr[i]]);
    }

    for (let i = k - 1; i < len; i++) {
        let idx = arr[i];
        total += quality[idx];
        pq.enqueue(quality[idx]);
        const totalc = (wage[idx] / quality[idx]) * total;
        ans = Math.min(ans, totalc);
        total -= pq.dequeue().element;
    }

    return ans;
};

修剪二叉搜索树 ⭐⭐

👉 Leetcode 链接-669在新窗口打开

给你二叉搜索树的根节点 root ，同时给定最小边界 low 和最大边界 high。通过修剪二叉搜索树，使得所有节点的值在[low, high]中。修剪树不应该改变保留在树中的元素的相对结构 (即，如果没有被移除，原有的父代子代关系都应当保留)。可以证明，存在唯一的答案。

所以结果应当返回修剪好的二叉搜索树的新的根节点。注意，根节点可能会根据给定的边界发生改变。

输入：root = [1,0,2], low = 1, high = 2
输出：[1,null,2]

function trimBST(
    root: TreeNode | null,
    low: number,
    high: number
): TreeNode | null {
    if (!root) return null;

    if (root.val < low) {
        return trimBST(root.right, low, high);
    } else if (root.val > high) {
        return trimBST(root.left, low, high);
    } else {
        root.left = trimBST(root.left, low, high);
        root.right = trimBST(root.right, low, high);
        return root;
    }
}

统计子串中的唯一字符 ⭐⭐⭐

👉 Leetcode 链接-828在新窗口打开

我们定义了一个函数 countUniqueChars(s) 来统计字符串 s 中的唯一字符，并返回唯一字符的个数。

例如：s = "LEETCODE" ，则其中 "L", "T","C","O","D" 都是唯一字符，因为它们只出现一次，所以 countUniqueChars(s) = 5 。

本题将会给你一个字符串 s ，我们需要返回 countUniqueChars(t) 的总和，其中 t 是 s 的子字符串。输入用例保证返回值为 32 位整数。

注意，某些子字符串可能是重复的，但你统计时也必须算上这些重复的子字符串（也就是说，你必须统计 s 的所有子字符串中的唯一字符）。

function uniqueLetterString(s: string): number {
    let map = new Map(),
        len = s.length,
        res = 0;

    for (let i = 0; i < len; i++) {
        let char = s[i];
        if (!map.has(char)) {
            map.set(char, [-1]);
        }
        map.get(char).push(i);
    }

    for (const [_, arr] of map.entries()) {
        arr.push(len);
        for (let i = 1; i < arr.length - 1; i++) {
            res += (arr[i] - arr[i - 1]) * (arr[i + 1] - arr[i]);
        }
    }

    return res;
}

寻找重复的子树 ⭐⭐

👉 Leetcode 链接-652在新窗口打开

给定一棵二叉树 root，返回所有重复的子树。

对于同一类的重复子树，你只需要返回其中任意一棵的根结点即可。

如果两棵树具有相同的结构和相同的结点值，则它们是重复的。

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */
let res: Array<TreeNode>;
let map: Map<string, number>;
function findDuplicateSubtrees(root: TreeNode | null): Array<TreeNode | null> {
    res = new Array<TreeNode>();
    map = new Map<string, number>();

    dfs(root);

    return res;
}

function dfs(root: TreeNode | null): string {
    if (!root) return " ";
    let key = root.val + "_";
    key += dfs(root.left);
    key += dfs(root.right);

    if (!map.has(key)) map.set(key, 1);
    else map.set(key, map.get(key) + 1);

    if (map.get(key) === 2) res.push(root);
    return key;
}

长数对链 ⭐⭐

👉 Leetcode 链接-646在新窗口打开

给出 n 个数对。在每一个数对中，第一个数字总是比第二个数字小。

现在，我们定义一种跟随关系，当且仅当 b < c 时，数对(c, d) 才可以跟在 (a, b) 后面。我们用这种形式来构造一个数对链。

给定一个数对集合，找出能够形成的最长数对链的长度。你不需要用到所有的数对，你可以以任何顺序选择其中的一些数对来构造。

考点

动态规划｜贪心

function findLongestChain(pairs: number[][]): number {
    // pairs.sort((a,b) => a[0] -b[0])

    // let len = pairs.length, dp = new Array(len).fill(1)

    // for(let i=0;i<len;i++){
    //     for(let j=0;j<i;j++){
    //         if(pairs[i][0] > pairs[j][1]){
    //             dp[i] = Math.max(dp[i], dp[j] + 1)
    //         }
    //     }
    // }

    // return dp[len -1]
    pairs.sort((a, b) => a[1] - b[1]);

    let count = 0,
        cur = -Infinity;

    for (let item of pairs) {
        if (cur < item[0]) {
            cur = item[1];
            count++;
        }
    }

    return count;
}

商品折扣后的最终价格

👉 Leetcode 链接-1475在新窗口打开

给你一个数组 prices，其中 prices[i] 是商店里第 i 件商品的价格。

商店里正在进行促销活动，如果你要买第 i 件商品，那么你可以得到与 prices[j] 相等的折扣，其中 j 是满足 j > i 且 prices[j] <= prices[i] 的最小下标，如果没有满足条件的 j，你将没有任何折扣。

请你返回一个数组，数组中第 i 个元素是折扣后你购买商品 i 最终需要支付的价格。

function finalPrices(prices: number[]): number[] {
    let ans = [],
        len = prices.length,
        stack = new Array(len).fill(0);

    for (let i = len - 1; i >= 0; i--) {
        while (stack.length && stack[stack.length - 1] > prices[i]) {
            stack.pop();
        }
        ans[i] =
            stack.length === 0
                ? prices[i]
                : prices[i] - stack[stack.length - 1];
        stack.push(prices[i]);
    }

    return ans;
}

提示

知识点：👉 单调栈在新窗口打开

验证栈序列

👉 Leetcode 链接-946在新窗口打开

给定 pushed 和 popped 两个序列，每个序列中的值都不重复，只有当它们可能是在最初空栈上进行的推入 push 和弹出 pop 操作序列的结果时，返回 true；否则，返回 false。

function validateStackSequences(pushed: number[], popped: number[]): boolean {
    let stack: number[] = [],
        len = pushed.length;

    for (let i = 0, j = 0; i < len; i++) {
        stack.push(pushed[i]);
        while (stack.length && stack[stack.length - 1] === popped[j]) {
            stack.pop();
            j++;
        }
    }

    return stack.length === 0;
}

最大相等频率 TODO：

👉 Leetcode 链接-1224在新窗口打开

层数最深叶子节点的和 TODO：BFS DFS

👉 Leetcode 链接-在新窗口打开

给你一棵二叉树的根节点 root，请你返回层数最深的叶子节点的和。

function deepestLeavesSum(root: TreeNode | null): number {
    let maxLevel = -1;
    let sum = 0;

    const dfs = (node, level) => {
        if (!node) return;

        if (level > maxLevel) {
            maxLevel = level;
            sum = node.val;
        } else if (level === maxLevel) {
            sum += node.val;
        }

        dfs(node.left, level + 1);
        dfs(node.right, level + 1);
    };

    dfs(root, 0);

    return sum;
}

设计循环双端队列 ⭐⭐

👉 Leetcode 链接-641在新窗口打开

设计实现双端队列。

实现 MyCircularDeque 类：

MyCircularDeque(int k)：构造函数，双端队列最大为 k。 boolean insertFront()：将一个元素添加到双端队列头部。如果操作成功返回 true，否则返回 false。 boolean insertLast()：将一个元素添加到双端队列尾部。如果操作成功返回 true，否则返回 false。 boolean deleteFront()：从双端队列头部删除一个元素。如果操作成功返回 true，否则返回 false。 boolean deleteLast()：从双端队列尾部删除一个元素。如果操作成功返回 true，否则返回 false。 int getFront() )：从双端队列头部获得一个元素。如果双端队列为空，返回 -1。 int getRear()：获得双端队列的最后一个元素。如果双端队列为空，返回 -1。 boolean isEmpty()：若双端队列为空，则返回 true，否则返回 false。 boolean isFull()：若双端队列满了，则返回 true，否则返回 false。

class MyCircularDeque {
    private statck: number[];
    private front: number;
    private end: number;
    private max: number;

    constructor(k: number) {
        this.max = k + 1;
        this.front = 0;
        this.end = 0;
        this.statck = [];
    }

    insertFront(value: number): boolean {
        if (this.isFull()) return false;

        this.front = (this.front - 1 + this.max) % this.max;
        this.statck[this.front] = value;

        return true;
    }

    insertLast(value: number): boolean {
        if (this.isFull()) return false;

        this.statck[this.end] = value;
        this.end = (this.end + 1) % this.max;

        return true;
    }

    deleteFront(): boolean {
        if (this.isEmpty()) return false;

        this.front = (this.front + 1) % this.max;

        return true;
    }

    deleteLast(): boolean {
        if (this.isEmpty()) return false;

        this.end = (this.end - 1 + this.max) % this.max;
        return true;
    }

    getFront(): number {
        if (this.isEmpty()) return -1;

        return this.statck[this.front];
    }

    getRear(): number {
        if (this.isEmpty()) return -1;

        return this.statck[(this.end - 1 + this.max) % this.max];
    }

    isEmpty(): boolean {
        return this.front === this.end;
    }

    isFull(): boolean {
        return (this.end + 1) % this.max === this.front;
    }
}

函数独占时间 ⭐⭐⭐

👉 Leetcode 链接-636在新窗口打开

function exclusiveTime(n: number, logs: string[]): number[] {
    const stack = [],
        ans = new Array(n).fill(0);

    for (let log of logs) {
        let logArray = log.split(":"),
            name = logArray[0],
            type = logArray[1],
            time = Number(logArray[2]);

        if (type === "start") {
            if (stack.length) {
                // 这里每个函数函数的起始值为 0
                ans[stack[stack.length - 1][0]] +=
                    time - stack[stack.length - 1][1];
                stack[stack.length - 1][1] = time;
            }
            stack.push([name, time]);
        } else {
            let peek = stack.pop();
            ans[peek[0]] += time - peek[1] + 1;

            if (stack.length) {
                stack[stack.length - 1][1] = time + 1;
            }
        }
    }

    return ans;
}

二叉树中增加一行

👉 Leetcode 链接-623在新窗口打开

给定一个二叉树的根 root 和两个整数 val 和 depth，在给定的深度 depth 处添加一个值为 val 的节点行。

注意，根节点 root 位于深度 1。

加法规则如下：

给定整数 depth，对于深度为 depth - 1 的每个非空树节点 cur，创建两个值为 val 的树节点作为 cur 的左子树根和右子树根。 cur 原来的左子树应该是新的左子树根的左子树。 cur 原来的右子树应该是新的右子树根的右子树。如果 depth == 1 意味着 depth - 1 根本没有深度，那么创建一个树节点，值 val 作为整个原始树的新根，而原始树就是新根的左子树。

/**
 * Definition for a binary tree node.
 * class TreeNode {
 *     val: number
 *     left: TreeNode | null
 *     right: TreeNode | null
 *     constructor(val?: number, left?: TreeNode | null, right?: TreeNode | null) {
 *         this.val = (val===undefined ? 0 : val)
 *         this.left = (left===undefined ? null : left)
 *         this.right = (right===undefined ? null : right)
 *     }
 * }
 */

function addOneRow(
    root: TreeNode | null,
    val: number,
    depth: number
): TreeNode | null {
    if (!root) return null;

    if (depth === 1) return new TreeNode(val, root, null);

    if (depth === 2) {
        root.left = new TreeNode(val, root.left, null);
        root.right = new TreeNode(val, null, root.right);
    } else {
        root.left = addOneRow(root.left, val, depth - 1);
        root.right = addOneRow(root.right, val, depth - 1);
    }

    return root;
}

非递增顺序的最小子序列

👉 Leetcode 链接-1403在新窗口打开

给你一个数组 nums，请你从中抽取一个子序列，满足该子序列的元素之和严格大于未包含在该子序列中的各元素之和。

如果存在多个解决方案，只需返回长度最小的子序列。如果仍然有多个解决方案，则返回元素之和最大的子序列。

与子数组不同的地方在于，“数组的子序列” 不强调元素在原数组中的连续性，也就是说，它可以通过从数组中分离一些 (也可能不分离) 元素得到。

function minSubsequence(nums: number[]): number[] {
    let res = [],
        sum = getSum(nums),
        len = nums.length,
        temp = 0;

    nums.sort((a, b) => b - a);

    for (let i = 0; i < len; i++) {
        temp += nums[i];
        res.push(nums[i]);

        if (temp * 2 > sum) {
            break;
        }
    }

    return res;
}

function getSum(nums: number[]) {
    return nums.reduce((pre, cur) => pre + cur);
}

有序队列 ⭐⭐

👉 Leetcode 链接-899在新窗口打开

给定一个字符串 s 和一个整数 k。你可以从 s 的前 k 个字母中选择一个，并把它加到字符串的末尾。

返回在应用上述步骤的任意数量的移动后，字典上最小的字符串。

提示

示例 1：
- 输入：s = “cba”，k = 1
- 输出：“acb”
- 解释：在第一步中，我们将第一个字符 (“c”) 移动到最后，获得字符串 “bac”。在第二步中，我们将第一个字符 (“b”) 移动到最后，获得最终结果 “acb。
示例 2： - 输入：s = “baaca”，k = 3 - 输出：“aaabc” - 解释：在第一步中，我们将第一个字符 (“b”) 移动到最后，获得字符串 “aacab”。在第二步中，我们将第三个字符 (“c”) 移动到最后，获得最终结果 “aaabc”。 :::

function orderlyQueue(s: string, k: number): string {
    if (k === 1) {
        let res = s;

        for (let i = 0; i < s.length - 1; i++) {
            const n = s.length;
            s = s.substring(1, n) + s[0];

            res = res < s ? res : s;
        }

        return res;
    }

    return [...s].sort().join("");
}

设计循环队列

👉 Leetcode 链接-622在新窗口打开

设计你的循环队列实现。循环队列是一种线性数据结构，其操作表现基于 FIFO (先进先出) 原则并且队尾被连接在队首之后以形成一个循环。它也被称为 “环形缓冲器”。

循环队列的一个好处是我们可以利用这个队列之前用过的空间。在一个普通队列里，一旦一个队列满了，我们就不能插入下一个元素，即使在队列前面仍有空间。但是使用循环队列，我们能使用这些空间去存储新的值。

你的实现应该支持如下操作：

MyCircularQueue(k)：构造器，设置队列长度为 k。 Front：从队首获取元素。如果队列为空，返回 -1。 Rear：获取队尾元素。如果队列为空，返回 -1。 enQueue(value)：向循环队列插入一个元素。如果成功插入则返回真。 deQueue()：从循环队列中删除一个元素。如果成功删除则返回真。 isEmpty()：检查循环队列是否为空。 isFull()：检查循环队列是否已满。

class MyCircularQueue {
    private length: number;
    private quene: number[];
    private head: number;
    private tail: number;

    constructor(k: number) {
        this.length = k;
        this.quene = new Array(k);
        this.head = 0;
        this.tail = 0;
    }

    enQueue(value: number): boolean {
        if (this.isFull()) return false;

        this.quene[this.tail % this.length] = value;
        this.tail++;

        return true;
    }

    deQueue(): boolean {
        if (this.isEmpty()) return false;
        this.head++;
        if (this.head === this.length) {
            this.head -= this.length;
            this.tail -= this.length;
        }

        return true;
    }

    Front(): number {
        return this.isEmpty() ? -1 : this.quene[this.head % this.length];
    }

    Rear(): number {
        return this.isEmpty() ? -1 : this.quene[(this.tail - 1) % this.length];
    }

    isEmpty(): boolean {
        return this.head === this.tail;
    }

    isFull(): boolean {
        return this.tail - this.head === this.length;
    }
}

Z 字形变换 (2022.7.29)

👉 Leetcode 链接-6在新窗口打开

将一个给定字符串 s 根据给定的行数 numRows，以从上往下、从左到右进行 Z 字形排列。

比如输入字符串为 “PAYPALISHIRING” 行数为 3 时，排列如下：

P   A   H   N
A P L S I I G
Y   I   R

之后，你的输出需要从左往右逐行读取，产生出一个新的字符串，比如：“PAHNAPLSIIGYIR”。

请你实现这个将字符串进行指定行数变换的函数：

function convert(s: string, numRows: number): string {
    if (numRows === 1) return s;

    const sLen = s.length;
    let len = Math.min(sLen, numRows),
        rows = [];

    for (let i = 0; i < len; i++) {
        rows[i] = "";
    }

    let start = 0,
        flag = false;

    for (let char of s) {
        rows[start] += char;

        if (start === 0 || start === numRows - 1) {
            flag = !flag;
        }

        start += flag ? 1 : -1;
    }

    let res = "";

    for (let row of rows) {
        res += row;
    }

    return res;
}

# 每日一题

# 最大网络秩

# 礼物的最大价值（动态规划）

# 得到 K 个黑块的最少涂色次数(滑动窗口)

# 保证文件名唯一

# 二进制数

# 堆叠长方体的最大高度

# 示例

# 思路

# 一个数字是否可以表示成三的幂的和

# 示例

# 思路

# 代码

# 最大频率栈

# 题目说明

# 输入输出

# 解题思路

# 代码实现

# 第 N 个神奇数字

# 题目说明

# 输入输出

# 解题思路

# 计算最小公倍数

# 代码实现

# 分汤

# 题目说明

# 输入输出

# 解题思路

# 动态规划部分

# 期望部分

# 代码实现

# 香槟塔

# 题目说明

# 输入输出

# 解题思路

# 代码实现

# 自定义字符串排序

# 题目说明

# 输入输出

# 解题思路

# 代码实现

# 解析布尔表达式

# 链表组件

# 按照频率将数组升序排序

# 两个相同字符之间的最长子字符串

# 最大交换

# 暴力解法

# 贪心解法 ⭐⭐

# 雇佣 K 名工人的最低成本 ⭐⭐⭐

# 修剪二叉搜索树 ⭐⭐

# 统计子串中的唯一字符 ⭐⭐⭐

# 寻找重复的子树 ⭐⭐

# 长数对链 ⭐⭐

# 商品折扣后的最终价格

# 验证栈序列

# 最大相等频率 TODO：

# 层数最深叶子节点的和 TODO：BFS DFS

# 设计循环双端队列 ⭐⭐

# 函数独占时间 ⭐⭐⭐

# 二叉树中增加一行

# 非递增顺序的最小子序列

# 有序队列 ⭐⭐

# 设计循环队列

# Z 字形变换 (2022.7.29)

每日一题

最大网络秩

礼物的最大价值（动态规划）

得到 K 个黑块的最少涂色次数(滑动窗口)

保证文件名唯一

二进制数

堆叠长方体的最大高度

示例

思路

一个数字是否可以表示成三的幂的和

示例

思路

代码

最大频率栈

题目说明

输入输出

解题思路

代码实现

第 N 个神奇数字

题目说明

输入输出

解题思路

计算最小公倍数

代码实现

分汤

题目说明

输入输出

解题思路

动态规划部分

期望部分

代码实现

香槟塔

题目说明

输入输出

解题思路

代码实现

自定义字符串排序

题目说明

输入输出

解题思路

代码实现

解析布尔表达式

链表组件

按照频率将数组升序排序

两个相同字符之间的最长子字符串

最大交换

暴力解法

贪心解法 ⭐⭐

雇佣 K 名工人的最低成本 ⭐⭐⭐

修剪二叉搜索树 ⭐⭐

统计子串中的唯一字符 ⭐⭐⭐

寻找重复的子树 ⭐⭐

长数对链 ⭐⭐

商品折扣后的最终价格

验证栈序列

最大相等频率 TODO：

层数最深叶子节点的和 TODO：BFS DFS

设计循环双端队列 ⭐⭐

函数独占时间 ⭐⭐⭐

二叉树中增加一行

非递增顺序的最小子序列

有序队列 ⭐⭐

设计循环队列

Z 字形变换 (2022.7.29)